Modulation of Schamel's nonlinear Schrödinger equation and related sheath excitations in degenerate relativistic quantum complex plasmas: A review

Abstract

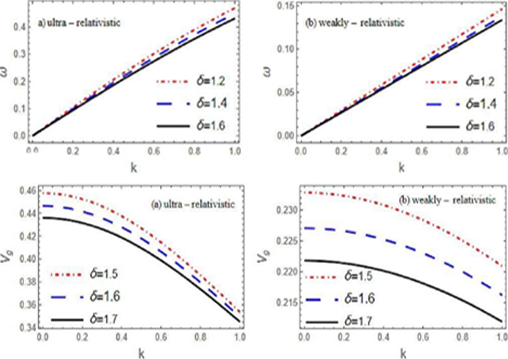
Degenerate relativistic quantum plasmas are intricate systems in which high-density electrons demonstrate relativistic and quantum mechanical properties. These conditions result in non-linear phenomena, such as soliton production, which are essential for energy transfer and stability analysis. The Schamel nonlinear Schrödinger equation offers a framework for examining wave dynamics in these conditions, integrating fractional non-linearities that elucidate modulation instability and envelope solitons. This study examines the impact of critical physical parameters, including the relativistic degeneracy ratio, ion trapping, and density ratio, on soliton dynamics. The results indicate that the relativistic degeneracy ratio strongly influences wave frequency, group velocity, and energy transport efficiency, particularly in ultra-relativistic plasmas. The research emphasizes the mitigating effects of heightened electron degeneracy pressure, which stabilises waves and diminishes soliton amplitude. The vortex-like arrangement of trapped ions enhances the non-linear dynamics of plasma. These findings enhance our comprehension of wave propagation, energy distribution, and stability in extreme plasma conditions.