On (f, g)-derivation in BCH-algebra
DOI:
https://doi.org/10.59190/stc.v1i3.196Keywords:
Axiom, BCH-Algebra, (f, g)-Derivation, (l, r)-(f, g)-Derivation, (r, l)-(f, g)-DerivationAbstract
BCH-algebra is a non-empty set with the binary operation * and the constant 0, and statisfying the certain axioms. A mapping of d from X to itself is said to be a derivation in BCH-algebra if d is both (l, r)-derivation and (r, l)-derivation in BCH-algebra, where X is BCH-algebra. This article discusses the concepts of (l, r)-(f, g)-derivation, (r, l)-(f, g)-derivation, and (f, g)-derivation in BCH-algebra, and investigates the properties (l, r)-(f, g)-derivation, (r, l)-(f, g)-derivation and (f, g)-derivation in BCH-algebra.
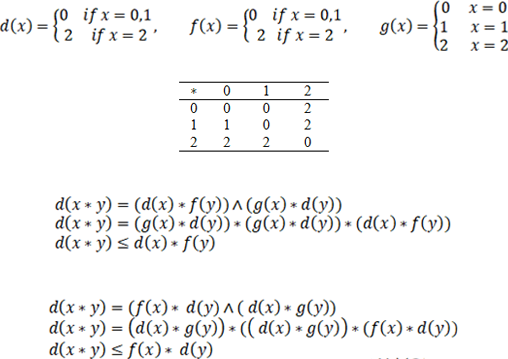
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2021 Sherly Afriastuti, Sri Gemawati, Syamsudhuha Syamsudhuha

This work is licensed under a Creative Commons Attribution 4.0 International License.










