A computational model of acoustic ray propagation in the deep-sound channel axis ocean region based on the Euler-Cromer method

Abstract

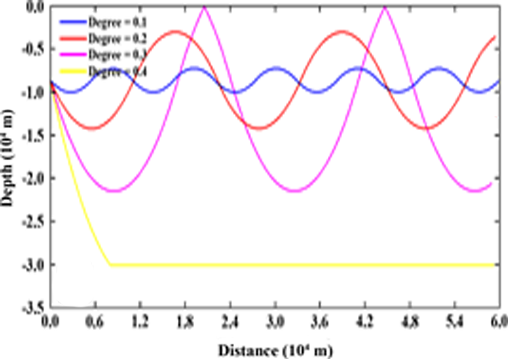
Research on the model of sound wave propagation in the ocean on the axis of the deep sound channel has been carried out using discrete acoustic ray propagation with varying beam lengths. This study aims to obtain parameter values in the form of maximum angle of incidence and effective beam length to simulate acoustic wave propagation around the axis of the deep sound channel. The research was conducted by simulating the acoustic beam at a depth with the minimum acoustic velocity value by varying the angle of incidence and the length of the applied beam. In this study, constant acoustic velocity gradient and gradient data were used. Calculation of the velocity gradient from discrete data using the Euler-Crommer formula. From this research, it can be seen that at a depth of 854 m the minimum acoustic velocity is 1487.53 m/s. For a constant gradient with a value of 0.054 and variations in beam length from 1 m to 4 m, the maximum angle of incidence is 0.4 radians. Analytically, the radius of curvature of the rays is 28107.12 m. Comparing the analysis and computation results, there is a very small error of 0.02%, so this model can be used to simulate acoustic wave propagation based on real data gradients. The gradient pattern based on real data and variations in beam length from 1 m to 4 m, obtained a maximum angle of incidence of 0.4 radians.